Najkontroverzniji aksiom svih vremena
Aksiom izbora objašnjen širem krugu čitatelja zainteresiranih za neka pitanja matematike

Ako vjerujete Banachu i Tarskom, možete uzeti jednu loptu, isjeći je na više dijelova, promiješati ih i spojiti ih u dvije potpune lopte jednake veličine.

Magično udvostručavanje lopte moglo bi razljutiti računovođe i inženjere...

no dokaz da se lopta može udvostručiti ne radi skoro ništa problematično.
Zapravo, najproblematičnija stvar koju moramo učiniti jest – izabrati.

Da! Ispostavlja se da je izabiranje kontroverznije nego što to se na prvu čini. Štaviše, aksiom izbora je vjerovatno najdiskutiraniji i najkontroverzniji aksiom koji postoji u matematici.
Kako bismo vas uvjerili da je izabiranje teško, osvrnimo se na jednostavan primjer, izbor broja između 0 i 1. Hajte, izaberite jedan!

Kao i djevojčica u crvenoj haljini, i vi ste vjerovatno izabrali racionalni broj, tj. razlomak. To nije nikakav problem, no, sjetite se da ne postoji baš mnogo racionalnih brojeva. Tako da hajdemo pokušati izabrati jedan nasumičan iracionalni broj između 0 i 1.
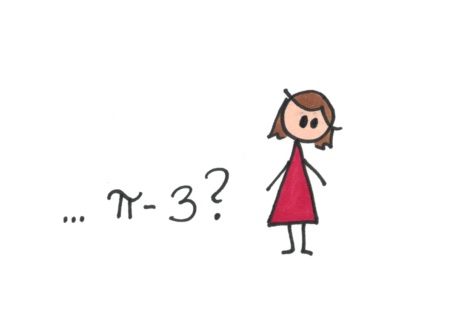
Postoji veliki broj mogućih izbora, poput π – 3, √2/3 ili ln(e – 2+1) no to u stvarnosti nije nasumičan iracionalni broj. Svi oni su više posebni brojevi koje možemo napisati koristeći fensi formule, nego što su u potpunosti nasumičan izbor.
Kako bismo onda mogli izabrati nasumičan broj?
Prisjetite se da iracionalan broj može biti zamišljen kao beskonačan decimalni broj, koji se ne ponavlja niti završava. Znači, da bismo nasumično izabrali iracionalan broj, trebali bismo nasumično izabrati cifre, jednu po jednu.

Odlično! Sada ste zaista izabrali nasumičan iracionalan broj!
Hajte, recite mi koji ste broj izabrali

Uočavate li problem?
Izabiranje jedne cifre, ili čak milion, nije tako teško (barem ne u teoriji). Imate cifre, izaberete jednu – nikakav problem.
No ukoliko morate napraviti beskonačan broj izbora... Dobro, lako je reći da biste trebali napraviti beskonačan broj izbora, no da li to možete i uraditi? Ukoliko mi ne možete reći koji ste broj izabrali, da li ste zaista izabrali broj?

U tome se sastoji kontroverza aksioma izbora.
Šta zapravo kaže aksiom izbora?
Aksiom izbora kaže da za bilo koju kolekciju (nepraznih) skupova, možete izabrati po jedan element iz svakog skupa.
Na primjer, da smo izabrali konačan decimalni broj, kao prethodno, naša kolekcija skupova bila bi gomila kopija skupa cifara između 0 i 9, jedan skup za svaki beskonačni broj cifara koje trebamo izabrati. Aksiom izbora kaže da možemo izabrati jednu cifru iz svakog skupa cifara kako bismo izabrali beskonačan decimalni broj. Ne kaže kako izabrati te cifre, ili koje cifre izabrati, samo kaže da ih možete nekako izabrati.

(Da razjasnimo, aksiom izbora ne govori o nasumičnim izborima, već o izboru općenito. Tako da u primjeru izbora cifara koji smo upravo iskoristili, aksiom izbora prosto kaže da postoji neki beskonačan decimalni broj koji možemo izabrati, a ne da se radi o nasumičnom broju. Za aksiom izbora u potpunosti je prihvatljivo izabrati, recimo, sve nule i završiti sa brojem 0.)
Zašto je onda ovaj aksiom tako kontroverzan?
Prvo, zato što zapravo ne možete pristupiti objektu/objektima koje je izabrao aksiom izbora.

Aksiomi obično predstavljaju osnovne definicije, ili bazične istine, ili nešto što je „očigledno“ istina. Na primjer, jedan drugi osnovni aksiom (teorije skupova) kaže da bez obzira na to koji (redni) broj izaberete, uvijek postoji i veći broj. To se čini poprilično očiglednim.
No, sa aksiomom izbora... Baš kao što mi niste mogli reći koji ste broj izabrali nasumično birajući svaku cifru, aksiom izbora prosto kaže da možete izabrati, ali ne kaže koji, niti kakav je taj izbor.
Ukoliko mi ne možete reći koji broj ste izabrali, da li ste ga onda izabrali?

Kako je „očigledno“ da možete napraviti takav izbor?
Ovo je argument konstruktivista. Prema njihovom mišljenju sve treba biti eksplicitno. Izbor jedino ima smisla ako mi možete reći šta ste izabrali, ili ako ništa, način na koji ste došli do tog jedinstvenog izbora. Aksiom izbora ne zadovoljava ovaj standard, tako da bismo ga trebali izbjeći.

Druga primjedba je ta da aksiom izbora vodi do niza „očigledno pogrešnih“ rezultata.
Kao što smo gore već spomenuli, jedna od najpoznatijih posljedica aksioma izbora je Banach-Tarskijev paradoks. Ukratko, kaže kako možete uzeti loptu, isjeći je na više dijelova, promiješati ih i sastaviti ih u dvije lopte koje su iste veličine kao original! Uistinu izgleda kao crna magija.
Problem je u tome što je aksiom izbora isto tako neizostavan za dobivanje ključnih, temeljnih, „očiglednih“ rezultata!
Na primjer, nema ništa očiglednije od toga da kada imate dvije kese riže, jedna ima više zrna od druge, ili možda imaju istu količinu riže.
Ali bez aksioma izbora ne možete reći to isto o skupovima!
Naravno, to nije problem sa konačnim skupovima. Skup 42 stvari veći je od onoga sačinjenog od 27 stvari. No kada govorimo o beskonačnim skupovima, nije uvijek baš najjasnije kako ih usporediti.
Problem se sastoji u tome što možete izmisliti dva komplicirana skupa A i B gdje nije očigledno kako usporediti stvari u skupu A sa stvarima iz skupa B. Štaviše, bez aksioma izbora možete pokazati da je ponekad nemoguće porediti veličine dva skupa. Nije da samo ne znate koji je veći. Još gore od toga. Oba skupa imaju veličine, ali ne možete čak ni usporediti njihove veličine.

Ispada da je reći da se veličina skupova uvijek može usporediti jednako aksiomu izbora. Drugim riječima, ili ćete prihvatiti aksiom izbora ili nećete baš uvijek moći usporediti veličine. Jedno ne ide bez drugoga.
Postoji mnogo drugih teorema ekvivalentnih aksiomu izbora. Možete pronaći čitav odjeljak na Wikipediji o aksiomu izbora gdje su izlistani neki od ekvivalentnih rezultata, od kojih su jedni više, a drugi manje intuitivni.

Da citiramo Jerryja Bona, „Aksiom izbora očigledno je istina; Princip dobrog uređenja je očigledno netačan; a ko može nešto reći o Zornovoj lemi?“ Šala se sastoji u tome što su svi oni zapravo ekvivalentni.
Sve ovo vodi do dva veoma značajna pitanja.
Prvo, ne možete „opovrgnuti“ aksiom s obzirom na to da su aksiomi osnovne pretpostavke. No, možete li dokazati da aksiom izbora nije konzistentan (neproturječan)?
Konzistentan skup aksioma je skup pretpostavki iz kojih se ne mogu dokazati kontradikcije (proturječja). Na primjer, ukoliko biste korištenjem vaših aksioma dokazali da je 0 jednako 1, to bi značilo da vaši aksiomi nisu konzistentni.
Ukoliko biste dokazali da aksiom izbora uzrokuje proturječja, sve računovođe ovoga svijeta osjetile bi olakšanje, s obzirom na to da bismo tada mogli odbaciti aksiom izbora i zajedno s njim njegove nemoguće posljedice kao što je Banach-Tarskijev paradoks.

Međutim, Gödel opet pristiže u pomoć. Gödel je 1940. godine pokazao da sam aksiom izbora ne dovodi ni do kakvih proturječja.
Dobro, to znači ne možemo odbaciti aksiom izbora zbog proturječja, ma koliko nam Banach-Tarskijev paradoks izazivao pometnju u glavi.
No možda možemo učiniti suprotno. Drugo pitanje u vezi sa aksiomom izbora je da li možemo dokazati njegovu tačnost koristeći samo druge aksiome. Drugim riječima, trebamo li uopće pretpostavljati aksiom izbora, ili ga dobivamo besplatno?
I ovdje isto tako dolazimo do zanimljivog odgovora. Cohen je 1963. godine dokazao da je nemoguće dokazati aksiom izbora polazeći od drugih, standardnih aksioma.
Šta to za nas, neustrašive istraživače matematike, znači?

Kao (ne-očigledna) posljedica, Cohenov dokaz znači da možemo slobodno pretpostaviti da je aksiom izbora tačan, ili da on zapravo nije tačan! I jedno i drugo je u redu za matematiku.
Kako se matematičari nose sa ovom kontroverzom?
U početku su matematičari odbijali aksiom izbora. Veoma je poznata priča kada je Tarski iskoristio aksiom izbora kako bi dokazao rezultat o veličini beskonačnih skupova. Predao je članak časopisu i kao odgovor – oba urednika su mu odbili članak.
Šta je bio njihov argument? Pa dobro, Fréchet je napisao da se korištenjem jedne dobro poznate istine da bi se dokazala druga dobro poznata istina ne dobiva nikakav novi rezultat. S druge strane, Lebesgue je napisao da ga korištenje jedne lažne tvrdnje da bi se dokazala druga uopće ne interesira.

Danas, međutim, većina matematičara prihvata aksiom izbora bez mnogo ustezanja. Jednostavno je isuviše koristan u dokazivanju isuviše temeljnih rezultata u mnogim poljima. Konzistentan je, tako da se čini da ne postoji niti jedan razlog radi kojeg se ne bi koristio, bez obzira na povremeni paradoks do kojeg dovodi.

Izvor: infinityplusonemath.wordpress.com
S engleskog prevela: Amina Turudija, Prometej.ba
