Neeuklidske geometrije - uzdrmavanje Kantove filozofije prostora
Piše: F.Šarčević Polazna točka Kantove filozofije prostora bila je nužna istinitost euklidske geometrije. Naime, znanje utemeljeno na iskustvu ne može biti nužno, odakle slijedi da prostorna intuicija kao izvorište nužno istinite euklidske geometrije mora biti neovisna o iskustvu. S Kantom ova intuicija postaje uvjetom same mogućnosti iskustva. (Z.Šikić) Međutim, u 19. stoljeću počinju se razvijati neeuklidske geometrije koje su uzdrmale tu osnovnu Kantovu tačku.
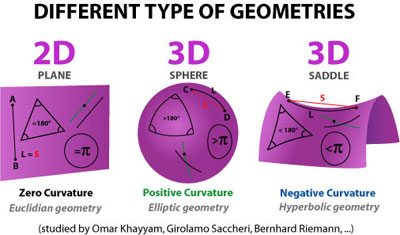
Da bismo predstavili značaj ovoga problema, moramo se prvo upoznati s pojmovima euklidske i neeuklidske geometrije, odnosno s onim o čemu one govore.
Geometrija se u primjeni koristila od početka ljudske civilizacije i prvotno je predstavljala razne sisteme mjerenja i premjeravanja zemljišta. Odatle i porijeklo riječi 'geometrija'. Nema sumnje da su graditelji babilonskih zdanja, egipatskih piramida i ostalih čuda starog vijeka bili kvalitetni geometri i matematičari. Ali, kao što smo pisali u prethodnim člancima, grčka filozofija kroz platonističko-aristotelovsku opreku, uz asistencije Elejaca i drugih koji su razmatrali ovaj problem, počela je razmatrati same temelje geometrije i pitanje njezine izvjesnosti i primjenjivosti. Da bi se broj tvrđenja u kojima moramo provesti poistovjećivanja s osjetilnim svijetom sveo na minimum, bilo je potrebno da se geometrija aksiomatizira. Objasnimo što znači aksiomatizacija.
Matematika odnosno geometrija specifične su po tome što su u potpunosti izgrađene deduktivno. (Istina, postoje induktivne metode, ali one predstavljaju matematičku indukciju koja je opet zasnovana na aksiomu, to jest nije empirijska.) Dakle, svaka tvrdnja dobiva se na osnovu prethodno dokazanih tvrdnji i uvedenih definicija. Svaka tvrdnja je dokazana i kada je to jednom učinjeno ona predstavlja istinu koja univerzalno važi i koja je vječna i nepromjenjiva. Dakle, tvrdnja n dokazana je pomoću prethodnih n-1 tvrdnji, treća tvrdnja dokazana je na osnovu druge, druga na osnovu prve. I što sada? Na osnovu čega je dokazana prva tvrdnja? U tom hodu unatrag kroz deduktivni put zasnivanja nužno dolazimo do tvrdnji koje važe za sebe i po sebi i koje se ne mogu dokazivati. Te početne tvrdnje nazivamo aksiomima. Dakle, aksiomi su polazne tvrdnje neke matematičke teorije koje se ne dokazuju već se uzimaju kao bazni elementi, na osnovu kojih se onda izgrađuje čitava teorija. Uglavnom, aksiomi su očigledni, dakle u skup aksioma uzimaju se one tvrdnje u koje nitko ne treba sumnjati.
Svaki skup aksioma treba zadovoljavati tri uvjeta. Poredano po strogosti zahtijevanja, ti uvjeti su: 1.neproturječnost – da se ne može na osnovu aksiomatskog sistema dokazati jedno tvrđenje i njemu suprotno tvrđenje, jer u tom slučaju je čitava teorija besmislena; 2.potpunost – da se svaka tvrdnja posmatrane teorije može dokazati (ili opovrći) na osnovu tog aksiomatskog sistema; 3.nezavisnost – da se nijedna tvrdnja postavljena za aksiom ne može dokazati na osnovu ostalih aksioma, jer u tom slučaju ju možemo izbaciti iz skupa aksioma i premjestiti u teoreme.
Prvu sistematsku aksiomatizaciju geometrije dugujemo Euklidu. On je postavio sistem od pet aksioma na osnovu kojih je nastojao izvesti svu geometriju. Ključan za ovu priču jest peti Euklidov postulat, koji u ekvivalentnoj formulaciji glasi ovako: Za svaki pravac a i tačku A koja ne pripada tom pravcu, postoji jedan i samo jedan pravac koji sadrži tačku A i paralelan je s pravcem a. Rekli bismo, očigledna činjenica.
Kroz stoljeća poslije matematičari su ispitivali prije svega nezavisnost ovog Euklidovog sistema aksioma, tj. nastojali su njegov peti postulat dokazati na osnovu prethodnih i tako ga premjestiti u teoreme. U tom nastojanju nitko nije uspio. Kako smo pisali prethodno, za Kanta je polazna točka filozofije prostora bila pretpostavka nužne istinitosti Euklidske geometrije.
Ali u 19. stoljeću dolazi do velikog obrata. Matematičari (Lobačevski, zatim Riemann) umjesto petog Euklidovog aksioma uvode aksiom koji u ekvivalentnoj formulaciji glasi ovako: Za svaki pravac a i tačku A koja ne pripada tom pravcu, postoje najmanje dva pravca koji sadrže tačku A i paralelni su s pravcem a. Rekli bismo, nimalo očita činjenica, neprihvatljiva! Na osnovu ovog aksioma izgrađeni su razni modeli neeuklidskih geometrija. Ispočetka, njih se prihvaćalo samo kao alternativne matematičke sustave, koji jesu logički konzistentni (sve tvrdnje izvedene su deduktivno na osnovu uzetih aksioma) ali koji su intuitivno neprihvatljivi i ne odgovaraju stvarnosti. Drugim riječima, ne znamo što ćemo s njima i čemu nam takve geometrije mogu poslužiti? Zar postoji mjesto gdje je zbir uglova u trokutu manji od 180 stupnjeva, gdje se nijedna simetrala stranice trokuta ne siječe s drugom i gdje pravac izgleda krivo? Imamo li potrebu za takvom geometrijom?
Potpunu aksiomatizaciju geometrije dugujemo njemačkom matematičaru Davidu Hilbertu, koji je postavio 20 aksioma euklidske geometrije, od kojih se prvih 19 odnosi na apsolutnu geometriju a 20.aksiom jest spomenuti peti Euklidov postulat. Sve tvrdnje koje se izvedu na osnovu ovih 19 aksioma važe u svakoj geometriji, a dvadeseti aksiom pravi razliku. Ukoliko za njega uzmemo aksiom Euklida dobivamo jednu geometriju – euklidsku, a ako uzmemo spomenuti aksiom Lobačevskog dobivamo neeuklidske geometrije.
Neki matematičari i fizičari (Helmholtz, Riemann i drugi) počinju shvaćati polako da te nove geometrije nisu samo alternativni sustavi nego i da predstavljaju znanje o fizičkom svijetu. Tako se odmah postavilo novo osnovne pitanje za filozofiju geometrije: koja je geometrija (ili koji njezin dio) nužna apriorna spoznaja? “Apriornu prirodu neke (grane) geometrije ustanovit ćemo ako (1) pronađemo aksiome iz kojih se svi njezini teoremi mogu izvesti logičkim dedukcijama i (2) pokažemo da ti aksiomi postavljaju uvjete same mogućnosti iskustva. U tom je obliku kantovsko pitanje postavio Russell potkraj 19. stoljeća.“ (Z.Š.) Kako Šikić dalje piše u svojoj kratkoj Filozofiji matematike, Russellov odabir pao je na projektivnu geometriju. On ju je prvi aksiomatizirao i pokušao dokazati nužnost tih aksioma kao temeljnih za naše spoznavanje svijeta.
Ubrzo nakon tog Russellovog pokušaja promijenila se bitno naša spoznaja svijeta. Einsteinovom teorijom relativnosti (posebno općom) ušli smo u shvaćanje zakrivljenosti prostora po sebi, u novo shvaćanje gravitacije (gravitacija nije sila i sila ne može djelovati na daljinu, gravitacija je izraz geometrije zakrivljenog prostora!) i s njom je i Russellov pokušaj pao u vodu. S time se i prestalo inzistirati na apriorizmu u geometriji (došlo je do diskreditacije apriorizma i samim tim uzdrmavanja kantov(sk)ih postavki o filozofiji prostora) i pokazalo se da različitim aspektima zbilje odgovaraju različite geometrije. Drugim riječima, različitim pojmovnim okvirima pripadaju različite geometrije. Euklidska geometrija dovoljna je za opisivanje pojava u zemaljskim razmjerima, dok astronomska fizika predstavlja drugi pojmovni okvir kojem odgovora druga geometrija, neeuklidska. Štoviše, matematička istraživanja u 20. vijeku pokazala su da jedna te ista vrsta iskustva može biti jednako valjano organizirana na temelju različitih geometrija, što je posebno istaknuo Henry Poincaré.
Tako je geometrija od apriorne spoznaje postala konvencijom.
Tako je geometrija od apriorne spoznaje postala konvencijom.
Povezani članci:
Zenonov paradoks - hoće li Ahilej stići kornjaču?
Matematika od Platona do Kanta
Kant u kontekstu filozofije matematike
Matematika od Platona do Kanta
Kant u kontekstu filozofije matematike
