Na prvi pogled, topologija izgleda kao neuobičajeno neprecizna grana matematike. Ona izučava plastelinske figure koje se mogu savijati, rastezati i sabijati bez ograničenja. Međutim, topolozi imaju određene restrikcije: nije dozvoljeno praviti ili uništavati rupe unutar figura. (Stari je vic da topolozi ne znaju razliku između šalice i đevreka, s obzirom da oboje imaju jednu rupu, pa stoga često umoče đevrek u šalicu.) Iako se ovo može činiti vrlo dalekim od algebarske strogosti, moćna ideja zvana homologija pomaže matematičarima da povežu ta dva svijeta.

Riječ „rupa“ ima mnoga značenja u svakodnevnom govoru – mjehurići, gumene trake i zdjele imaju različite vrste rupa. Topologe, između ostaloga, zanima detektiranje jedne specifične vrste rupa, koje se mogu opisati kao zatvoren i šupalj prostor. Jednodimenzionalne rupe izgledaju poput gumenih traka. Vijugava linija koja formira traku je zatvorena (za razliku od opuštenog konca) i šuplja (za razliku od oboda novčića).

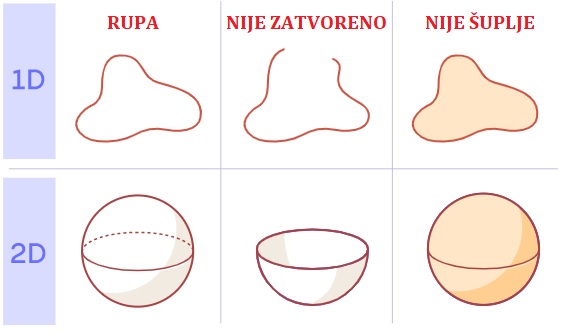
Proširujući ovu logiku, dvodimenzionalne rupe izgledaju kao šuplje lopte. Ove vrste rupa – zatvorene i šuplje – nalaze se u košarkaškim loptama, ali ne i u zdjelama ili kuglama za kuglanje.

Razmišljati o rupama na ovaj način može pomoći našoj intuiciji; međutim, matematika je stroga i precizna, pa se ništa od gore rečenog ne može prihvatiti kao matematička definicija. Na ovaj način ne možemo jasno opisati rupe u višim dimenzijama, na primjer, i ne možemo programirati kompjutor koji bi raspoznavao zatvorene i šuplje prostore.

„Ne postoji dobra definicija rupe“, kaže topolog Jose Perea s državnog Univerziteta u Michiganu.

Umjesto toga, homologija prepoznaje rupe u objektima pomoću njihovih granica, što je mnogo precizniji matematički koncept. Da bi izučavali rupe u objektu, matematičari samo trebaju informacije o njihovim granicama.

Granica figure je kolekcija tačaka na njezinoj periferiji. Ta granica je uvijek za jednu dimenziju manja od dimenzije same figure. Na primjer, granica jednodimenzionalne dužine sastoji se od dviju tačaka s jednog i drugog kraja. (Tačke smatramo nula-dimenzionalnima.) Granica punog trokuta je prazni trokut, koji se sastoji od jednodimenzionalnih stranica. Slično, puna piramida je ograničena šupljom piramidom.

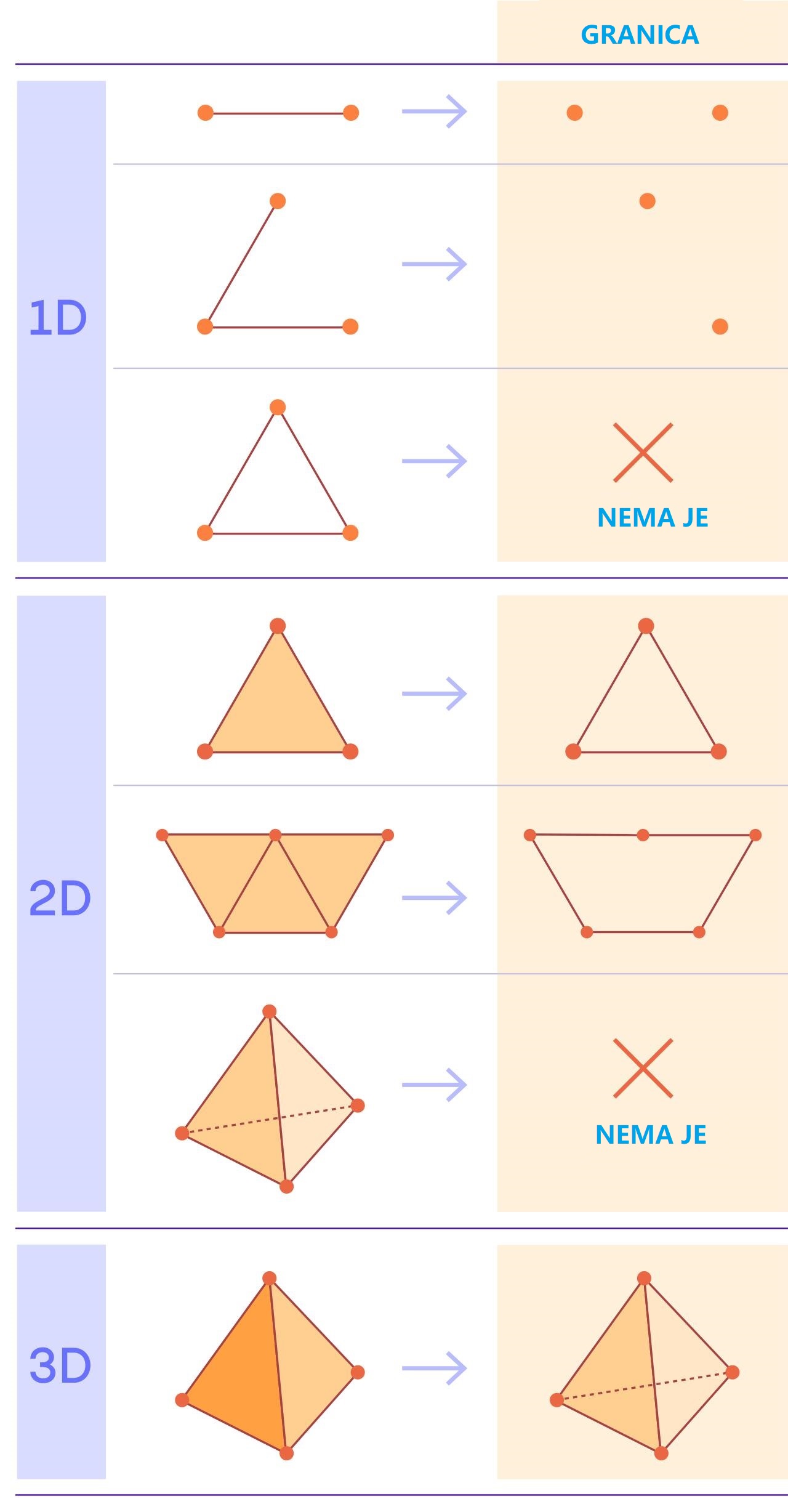
Ako zalijepite dvije dužine tako da kraj jedne bude početak druge, granična tačka u kojoj se te dvije dužine sreću nestaje. Granične tačke su poput ruba litice – blizu su tome da otpadnu s linije. Ali kada povežete linije, tačke koje su bile na ivicama su sada sigurne u centru. Ove dvije linije imaju ukupno četiri granične tačke, ali kada su zalijepljenje, rezultirajuća figura ima samo dvije granične tačke.

Ako možete prikačiti treću stranicu i zatvoriti strukturu, praveći tako šupalj trokut, tada granične tačke u potpunosti nestaju. Svaka granična tačka jedne stranice poništava se s tačkom drugom stranice, tako da šupalj trokut ostaje bez granice. Tako, kad god kolekcija linija formira petlju, granice se poništavaju.

Petlja završava u istoj tački u kojoj i počinje, ograđujući tako jednu oblast. Ali petlja formira rupu samo ako je ta oblast šuplja, kao što je slučaj s gumenom trakom. Kružnica nacrtana na papiru formira petlju, ali to nije rupa zato što je prostor unutar ispunjen. Petlje koje omeđuju punu oblast – od vrste koja nije rupa – su granica dvodimenzionalne oblasti.

Odatle, rupe imaju dvije važne rigorozne značajke. Prva, rupa nema granice, zato što ona formira zatvorenu figuru. Drugo, rupa nije granica ničega drugog, zato što rupa po sebi mora biti šuplja.

Ova definicija može se proširiti na više dimenzije. Dvodimenzionalni puni trokut je ograničen trima stranicama. Ako prikvačite nekoliko trokutova jedne na druge, neke granične stranice nestaju. Kada se četiri trokuta rasporede u piramidu, svaka od stranica se poništava s nekom drugom. Tako zidovi piramide nemaju granicu. Ako je ova piramida šuplja – to jest, ako nije granica trodimenzionalnog punog bloka – tada ona formira dvodimenzionalnu rupu.

Da bi našli sve tipove rupa unutar jedne topološke figure, matematičari grade nešto što se zove lančani kompleks, koji je skela za gradnju homologije.

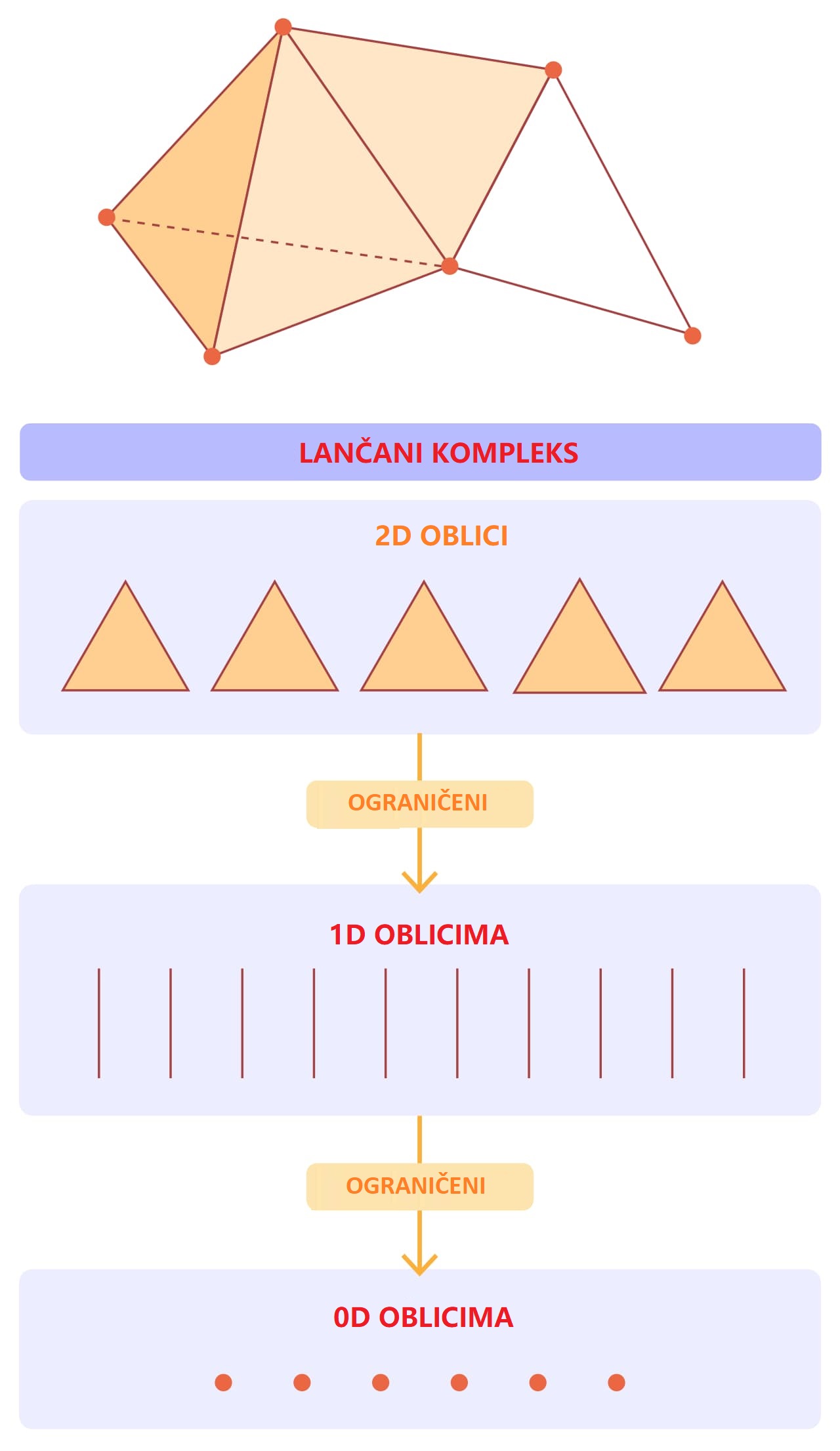
Mnoge topološke figure mogu se izgraditi lijepljenjem dijelova različitih dimenzija. Lančani kompleks je dijagram koji daje upute za sklapanje figure. Pojedinačni dijelovi figura grupiraju se po dimenzijama i onda se slažu hijerarhijski: prvi nivo sadrži sve tačke, sljedeći nivo sadrži sve linije, i tako dalje. Tu je također i prazni nulti nivo, koji služi samo kao temelj. Svaki nivo je povezan strelicama s onim ispod sebe, što ukazuje na to kako su zalijepljeni. Na primjer, puni trokut je povezan s tri stranice koje čine njegovu granicu.

Matematičari izdvajaju homologiju figure iz njezinog lančanog kompleksa, koji pruža strukturalne podatke o sastavnim dijelovima figure i njihovim granicama – upravo ono što treba da se opišu rupe u svakoj dimenziji. Kada koristite lančani kompleks, procesi za pronalaženje 10-dimenzionalne rupe i 1-dimenzionalne rupe su gotovo jednaki, bez obzira što je prvu mnogo teže vizualizirati nego drugu.

Definicija homologije je dovoljno stroga i precizna da je kompjutor može koristiti kako bi pronalazio i brojao rupe, što pomaže da se uspostavi strogoća koju matematika uvijek zahtijeva. To također omogućuje istraživačima da koriste homologiju za jednu rastuće popularnu namjenu: obradu podataka.

To je moguće zato što se podaci mogu vizualizirati kao tačke koje plutaju prostorom. Ove tačke podataka mogu predstavljati lokacije fizičkih predmeta, poput senzora, ili pozicije u apstraktnom prostoru, poput opisa preferencija u vezi hrane, gdje obližnje tačke upućuju na ljude koji imaju sličan ukus.

Da bi formirali figure iz podataka, matematičari crtaju linije između susjednih tačaka. Kada su tri tačke blizu, od njih se pravi puni trokut. Kada veći brojevi tačaka čine klaster, one formiraju kompliciranije i višedimenzionalne oblike. Popunjavanje tačaka podataka daje im teksturu i volumen – to je kreiranje slike iz točkica.

Homologija prevodi ovaj svijet maglovitih oblika u rigorozni jezik algebre, grane matematike koja izučava određene brojevne strukture i simetrije. Matematičari izučavaju osobine ovih algebarskih struktura u polju poznatom kao homološka algebra. Iz algebre oni indirektno dobivaju informacije o originalnim topološkim figurama podataka. Homologija dolazi u različitim oblicima, a svaki od njih je povezan s algebrom.

„Homologija je familijarna konstrukcija. Imamo mnogo algebarskih stvari koje znamo u vezi nje“, kaže Maggie Miller, postdoktorandica s MIT-a.

Informacija izvedena iz homologije tolerantna je i na nepreciznost u podacima: ako se podaci malkice promijene, broj rupa treba ostati isti. I kada se veći iznos podataka procesira, rupe mogu otkriti važne osobine. Na primjer, petlje u podacima koji se vremenski razlikuju mogu upućivati na periodičnost. Rupe u drugim dimenzijama mogu pokazati klastere ili praznine u podacima.

„Postoji stvarna potreba za robusnim metodama koje iz podataka izvlače kvalitativne osobine“, kaže Robet Ghrist s Univerziteta u Pennsylvaniji. „To je ono što vam homologija daje.“

Izvor: Quanta Magazine

S engleskog preveo: Franjo Šarčević, Prometej.ba